Featured image of post 2017-2018 ACM-ICPC, NEERC, Moscow Subregional Contest
CP NYCU_gAwr_gurA NYCU PCCA

2017-2018 ACM-ICPC, NEERC, Moscow Subregional Contest

Practice

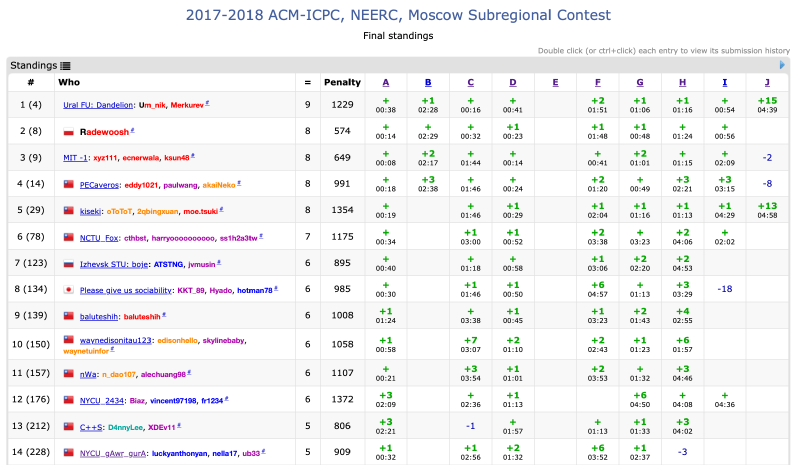
Standing

Solution

A. Advertising Strategy

題意

總共有 $n$ 個人，你想要讓所有人都看到影片
但你只能最多直接推給 $k$ 個人看影片
$a_i$ 表示第 $i$ 天看過影片的人數
$x_i$ 表示你在第 $i$ 天推給 $x_i$ 個人看影片
$\sum x_i <= k$
每天人數會倍增但最多增加沒看過的一半
Let $b_i = a_i + x_i$
$a_{i+1} = b_i + \min(b_i, \lfloor\frac{n-b_i}{2}\rfloor$)
求 $\min i$ 滿足 $a_i = n$
$n \le 10^{18}, k \le 10^{5}$

作法

如果要推影片 越早推越好 剩下的在最後一天推剩下的所有人 暴力枚舉一開始要推幾個人 複雜度是 $\mathcal{O}(k\log{n})$

submission
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;

signed main() {
    fast;

    ll n, k;
    cin >> n >> k;

    auto solve = [&](ll init) {
        ll a = 0; int d = 0;
        ll bound = n - (k - init);
        while (a < bound) {
            auto b = a;
            if (d == 0) b += init;
            a = b + min(b, (n-b)/2);
            d++;
        }
        return d+1;
    };

    int ans = 500;
    if (n <= k) ans = 1;
    for (int i = 1; i < k; i++) {
        auto x = solve(i);
        if (x < ans) ans = x;
    }
    cout << ans << endl;

    return 0;
}

B. Byteland Trip (TODO)

題意

有 $n$ 個星球
每個星球只能往一個方向走 $<$ or $>$
星球 $i$ 是 $<$ 表示可以去 $j < i$ （$>$ 則是 $j > i$）
對於每個星球 求它是終點的 TSP 路徑數量
$n \le 3000, \mod 10^9+7$

作法 (TODO)

聽說是 dp

C. Carpet

題意

給你一顆 $n$ 個點的樹
你要把這顆樹平放到 $1 000 000 \times 20$ 的平面上
保證邊不會重疊
$n \le 10^{5}$

作法

$2^{20} > 1e6$
輕重鏈剖分
依照 dfs 順序排列，先走輕點

WA1: 模板打錯字、沒先走輕點

submission
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;

constexpr int MAXN = 1e5+5;

struct HLD {
    int n, t, et, ulink[MAXN], deep[MAXN],
      mxson[MAXN], sz[MAXN], pa[MAXN], pl[MAXN],
      data[MAXN], dt[MAXN], bln[MAXN], edge[MAXN];
    vector<pii> G[MAXN];
    void init(int _n) {
        n = _n, t = 0, et = 1;
        for (int i = 1; i <= n; i++)
            G[i].clear(), mxson[i] = 0;
    }
    void add_edge(int a, int b, int w) {
        G[a].emplace_back(b, et);
        G[b].emplace_back(a, et);
        edge[et++] = w;
    }
    void dfs(int u, int f, int d) {
        sz[u] = 1, pa[u] = f, deep[u] = d++;
        for (auto [v,id]: G[u])
            if (v != f) {
                dfs(v, u, d), sz[u] += sz[v];
                if (sz[mxson[u]] < sz[v]) mxson[u] = v;
            } else bln[id] = u, dt[u] = edge[id];
    }
    void cut(int u, int link) {
        data[pl[u] = t++] = dt[u], ulink[u] = link;
        if (!mxson[u]) return;
        cut(mxson[u], link);
        for (auto [v,id]: G[u])
            if (v != pa[u] and v != mxson[u])
                cut(v, v);
    }
    void build() { dfs(1, 1, 1), cut(1, 1); }
};

int n;
HLD hld;
int X;
vector<pii> ans;

void dfs(int c, int d = 1) {
    if (hld.ulink[c] != hld.ulink[hld.pa[c]])
        d++;
    ans[c-1] = { X++, d };
    for (auto [x,id]: hld.G[c])
        if (x != hld.pa[c] and x != hld.mxson[c])
            dfs(x, d);
    if (hld.mxson[c])
        dfs(hld.mxson[c], d);
}

signed main() {
    fast;

    cin >> n;
    hld.init(n);
    for (int i = 1; i < n; i++) {
        int u, v; cin >> u >> v;
        hld.add_edge(u, v, 0);
    }
    hld.build();

    X = 1;
    ans.resize(n);
    dfs(1);

    for (auto [x,y]: ans)
        cout << x _ y << endl;

    return 0;
}

D. Decoding of Varints

題意

給你一個序列 $a$
連續的幾個數字會構成一個數字（題目的公式）
如果 $a_i<128$ 代表數字的結尾， 輸出每個數字
$n \le 10^5$

作法

簡單實作 注意 overflow 🫠

WA12: overflow

submission
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
using LL = __int128;

signed main() {
    fast;

    cerr _ "meow" _ endl;

    int n; cin >> n;
    vector<LL> ans;
    LL cur = 0;
    LL p = 1;
    for (int i = 0; i < n; ++i) {
        ll x; cin >> x;
        if (x < 128) {
            cur = cur + x * p;
            ans.push_back(cur);
            cur = 0;
            p = 1;
        } else {
            cur = cur + (x-128) * p;
            p = p * 128;
        }
    }
    for (auto &x : ans) {
        ll r;
        if (x % 2 == 0)
            r = x / 2;
        else
            r = -((x+1)/2);
        cout << r << '\n';
    }
    return 0;
}

E. Empire History (TODO)

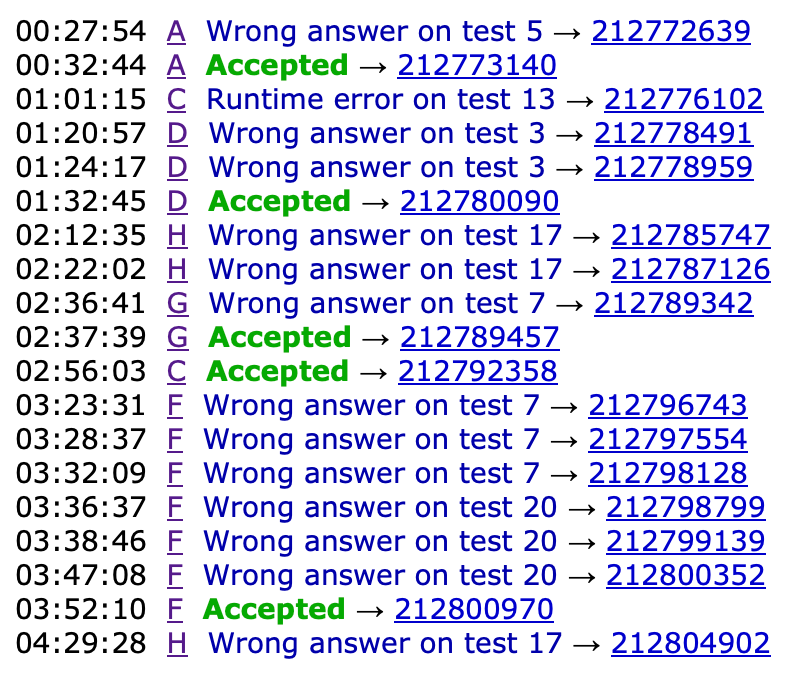
F. Fake or Leak?

題意

給你封版的記分板
和偷出來最終記分板的連續 $k$ 個
問你偷的記分板是不是假的

解法

判斷不在 leak 計分板的隊伍是否一定會在 $k$ 個隊伍之間。

WA123: 沒注意計分板保證合法 & 沒衝突
WA456: 沒判斷隊伍的可能範圍

submission
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;

struct Team {
    int solve, penalty, last, wa;
    string name;
};

bool operator<(Team a, Team b) {
    if (a.solve != b.solve)
        return a.solve > b.solve;
    if (a.penalty != b.penalty)
        return a.penalty < b.penalty;
    if (a.last != b.last)
        return a.last < b.last;
    return a.name < b.name;
}

int n,m,k;
char cc[2222][26];
int aa[2222][26], tt[2222][26];
Team team[2222];
string name[2222];
map<string, int> id;
set<int> leak;

Team mn(Team t) {
    auto add = n - t.solve;
    t.penalty += t.wa * 20 + add * 240;
    t.solve += add;
    t.last = 240;
    t.wa = 0;
    return t;
}
Team mx(Team t) {
    return t;
}

signed main() {
    fast;

    cin>>n>>m>>k;
    for(int i=0;i<m+k;i++)
    {
        cin>>name[i];
        if (i < m)
            id[name[i]]=i;
        else
            leak.insert(id[name[i]]);
        for(int j=0;j<n;j++)
        {
            cin>>cc[i][j]>>aa[i][j]>>tt[i][j];
        }
    }

    for (int i = 0; i < m+k; i++) {
        int solve = 0, penalty = 0, last = 0, wa = 0;
        for (int j = 0; j < n; j++)
            if (cc[i][j] == '+') {
                solve++;
                penalty += (aa[i][j] - 1) * 20 + tt[i][j];
                last = max(last, tt[i][j]);
            } else {
                wa += aa[i][j];
            }
        team[i].solve = solve;
        team[i].penalty = penalty;
        team[i].last = last;
        team[i].wa = wa;
        team[i].name = name[i];
    }

    for(int i = 1; i < m; i++)
        assert(team[i-1] < team[i]);
    for(int i = m+1; i < m+k; i++)
        assert(team[i-1] < team[i]);

    bool flag = 0;
    for(int i = 0; i < m; i++)
        if (leak.count(i) == 0 and team[m] < mn(team[i]) and mx(team[i]) < team[m+k-1])
            flag = 1;

    cout << (flag ? "Fake" : "Leaked") << endl;

    cerr _ "meow" _ endl;

    return 0;
}

G. God of Winds

題意

給你 $n \times m$ 的方格圖 （上下相連、左右相連）
每條邊有一個風向
垂直 +下-上、水平 +右-左
你可以加任意個 cyclone / anticyclone
問能不能達成輸入給定的風向

作法

  • 尤拉迴路
    • 所有點入度 = 出度
  • row (column) sum = 0

WA1: 沒判斷 sum = 0

submission
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;

signed main() {
    fast;

    int n, m;
    cin >> n >> m;
    vector<int> vc(n*m), vr(n*m);
    auto id = [&](int x, int y) {
        return x * m + y;
    };
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> vr[id(i,j)] >> vc[id(i,j)];

    bool can = true;

    for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) {
        auto pi = (i-1+n)%n;
        auto pj = (j-1+m)%m;
        ll sum = vc[id(i,j)] - vc[id(pi,j)] + vr[id(i,j)] - vr[id(i,pj)];
        can &= sum == 0;
    }

    //*
    for (int i = 0; i < n; i++) {
        ll sum = 0;
        for (int j = 0; j < m; j++)
            sum += vc[id(i,j)];
        can &= sum == 0;
    }
    for (int j = 0; j < m; j++) {
        ll sum = 0;
        for (int i = 0; i < n; i++)
            sum += vr[id(i,j)];
        can &= sum == 0;
    }
    //*/

    cout << (can ? "Yes" : "No") << endl;

    return 0;
}

H. Hilarious Cooking (upsolve)

題意

廚師要烤肉
$t_i$ 表示時間 $i$ 的溫度
問你能不能做到以下條件

  • 需要總共 $T$ 的溫度 $\sum t_i = T$
  • $| t_i - t_{i-1} | <= 1$
  • 有 $m$ 個條件
    • $t_{a_i} = b_i$

作法

把 $n$ 個溫度切成 $m+1$ 段
看每一段的上下界
需要注意實作細節

edge case 1
1
2
3

3 3 2
1 0
3 0
edge case 2
1
2
3

13 5 2
1 1
5 1
submission
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

#include <bits/stdc++.h>
using namespace std;

#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
using pll = pair<ll,ll>;

ll sum(ll a, ll b) {
    if (a > b) return 0;
    return (b - a + 1) * (a + b) / 2;
}

ll smin(ll x, ll w) {
    return sum(max(0ll, x-w), x-1);
}

ll smax(ll x, ll w) {
    return sum(x+1, x+w);
}

ll tri(ll w) {
    // 0 | 1 2 2 1 | 0
    // 0 | 1 2 3 2 1 | 0
    ll r = sum(1, w/2) * 2;
    if (w % 2)
        r += 1 + w / 2;
    return r;
}

signed main() {
    fast;

    ll T, n, m;
    cin >> T >> n >> m;
    vector<pll> v(m);
    for (auto &[a,b]: v)
        cin >> a >> b;

    ll sumT = 0;
    for (auto &[a,b]: v)
        sumT += b;
    ll tL = sumT, tR = sumT;

    bool can = true;

    for (int i = 1; i < m; i++) {
        auto [lx,ly] = v[i-1];
        auto [rx,ry] = v[i];
        auto mny = min(ly,ry), mxy = max(ly,ry);
        auto d = mxy - mny, w = rx - lx;
        auto sz = w-d-1;
        cerr _ w _ d _ sz _ endl;
        if (w < d) {
            can = false;
            break;
        } else if (d == w) {
            if (d > 1) {
                tL += (ly+ry) * (d-1) / 2;
                tR += (ly+ry) * (d-1) / 2;
            }
        } else {
            tL += (ly+ry-1) * d / 2;
            tR += (ly+ry+1) * d / 2;
            auto lsz = min(mny * 2, sz);
            tL += mny * lsz - tri(lsz);
            tR += mxy * sz + tri(sz);
        }
    }

    if (can) {
        tL += smin(v[0].sd, v[0].ft-1) + smin(v[m-1].sd, n-v[m-1].ft);
        tR += smax(v[0].sd, v[0].ft-1) + smax(v[m-1].sd, n-v[m-1].ft);
        cerr _ tL _ tR _ endl;
        can &= tL <= T and T <= tR;
    }

    cout << (can ? "Yes" : "No" ) << endl;

    return 0;
}

I. Infinite Gift (TODO)

題意

給 $k$ 維的無限整數格子點地圖 給 $n$ 個的向量 $v_i$
每個整數點 $a$ 會跟所有 $a+v_i$ 建邊
問你是否存在點著色，讓每條邊的兩端不同色
（等價於問是否為二分圖 or 問是否存在奇環）
$n,k<=1500$

作法 (TODO)

聽說是高斯消去

J. Judging the Trick (TODO)

題意

給長方形地圖範圍和 $n$ 個三角形
找出任意一個不在三角形裡（含邊上）的點
$n \le 10^5$

作法 (TODO)

可能可以掃描線

© 2021 - 2024 nella17's notes
Built with Hugo
Theme Stack designed by Jimmy