Practice
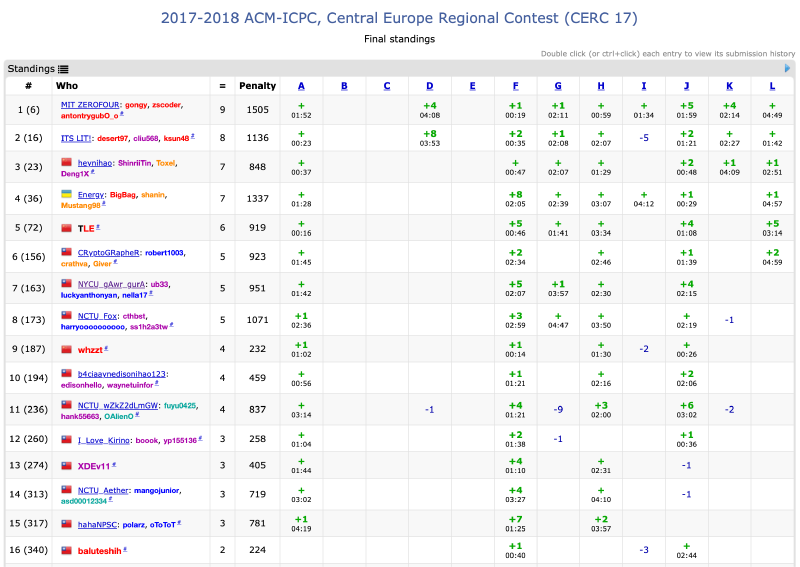
Standing
Solution
官解的簡報非常完整
只會 easy 和 medium 🫠

A. Assignment Algorithm
題意
給你飛機可選的座位表和規則
問你 $n$ 個人會怎麼選座位
作法
簡單實作
submission
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
| #include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
int vy[] = {
0, 1, 2,
4, 5, 6,
8, 9, 10,
};
int py[] = {
4, 2, 0, 5, 1
// 6, 8,10, X, 9
};
signed main() {
fast;
int r, n;
cin >> r >> n;
vector<string> mp(r+3);
for (auto &s: mp) cin >> s;
auto dist = [&](int row) {
return min({
abs(row - 0),
abs(row - (r/2+1)),
abs(row - (r+2))
});
};
for (int i = 0; i < n; i++) {
char c = 'a' + i;
vector<pii> vrow{};
for (auto x: { 1, r/2+2 }) {
int cnt = 0;
for (auto y: vy)
if (mp[x][y] == '-')
cnt++;
if (cnt)
vrow.emplace_back(x, cnt);
}
if (vrow.empty())
for (int x = 0; x < r+3; x++) {
int cnt = 0;
for (auto y: vy)
if (mp[x][y] == '-')
cnt++;
if (cnt)
vrow.emplace_back(x, cnt);
}
int row = max_element(ALL(vrow), [&](pii x, pii y){
if (x.sd != y.sd)
return x.sd < y.sd;
auto dx = dist(x.ft), dy = dist(y.ft);
if (dx != dy)
return dx > dy;
return x.ft > y.ft;
})->ft;
auto& srow = mp[row];
int elc = 0, erc = 0;
for (int x = 0; x < r+3; x++)
for (auto y: vy)
if (mp[x][y] == '-')
if (y != 5)
(y < 5 ? elc : erc)++;
for (auto ly: py) {
auto ry = 10 - ly;
auto ely = srow[ly] == '-';
auto ery = srow[ry] == '-';
if (!ely and !ery) continue;
if (ly != ry and ely and ery) {
if (elc >= erc)
srow[ly] = c;
else
srow[ry] = c;
} else if (ely) {
srow[ly] = c;
} else if (ery) {
srow[ry] = c;
}
break;
}
}
for (auto s: mp)
cout << s << endl;
return 0;
}
|
B. Buffalo Barricades (TODO)
C. Cumulative Code (TODO)
D. Donut Drone (TODO)
題意
給一張網格圖 每個格子有數字
上下互通 左右互通
每個點走一步會往右走 $y,y\pm1$ 最大那格
求 $m$ 筆操作
從某個點走 $k$ 步會走去哪
或改變一個數字
- grid $\le 2000 \times 2000$
- $m \le 5000$
- $k \le 10^9$
作法 (TODO)
E. Embedding Enumeration (TODO)
F. Faulty Factorial
題意
給 $n,p,r$
問是否能選兩個數字 $k, v$
滿足$2\le k \le n, 1 \le v \lt k$
$\displaystyle n! \frac{v}{k} \equiv r \mod p$
$2\le n \le 10^{18}, 2 \le p < 10^7$
作法
分 case
- $2p \le n$
then 有解 iff $r = 0$ - $p \le n \lt 2p$
then $k = p$ - $n \lt p$
then 枚舉 $k$
但算 $n$ 個模反元素 $k^{-1}$ 會太慢
可以轉換一下 只要算 $(n!)^{-1}$
WA12: 沒考慮到 edge case 1
WA3: 沒考慮到 edge 2
TLE4+MLE5: 算太多模反元素
edge case 1
edge case 2
submission
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
| #include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ull = unsigned ll;
using ld = long double;
using pii = pair<int,int>;
auto extgcd(ll a, ll b) {
ll s = 1, t = 0, u = 0, v = 1;
while (b) {
ll q = a / b;
swap(a -= q * b, b);
swap(s -= q * t, t);
swap(u -= q * v, v);
}
return tuple{ s, u, a }; }
ll inverse(ll x, ll p) {
auto a = get<0>(extgcd(x, p));
return a < 0 ? a + p : a;
}
ull modmul(ull a, ull b, ull M) {
ll ret = a * b - M * ull(1.L / M * a * b);
return ret + M * (ret < 0) - M * (ret >= (ll)M);
}
constexpr int MAXN = 3e7;
signed main() {
fast;
ll n, p, r;
cin >> n >> p >> r;
ll k = -1, v = -1;
if (n >= 2 * p or r == 0) {
if (r == 0 and n >= p and n != 2) {
if (p != 2)
k = 2, v = 1;
else
k = 3, v = 1;
}
} else if (n >= p) {
ll pd = 1;
for (int i = 1; i <= n; i++)
if (i != p)
pd = pd * i % p;
auto inv = inverse(pd, p);
cerr _ pd _ p _ inv _ endl;
auto uu = r * inv % p;
if (uu < p)
k = p, v = uu;
} else {
ll fact = 1;
for (int i = 1; i <= n; i++)
fact = fact * i % p;
auto invfact = inverse(fact, p);
// r/(n!/i) = r * i / n!
auto tt = r * invfact % p;
for (int i = 2; i <= n; i++) {
auto uu = tt * i % p;
if (uu < i) {
k = i, v = uu;
break;
}
}
}
cout << k _ v << endl;
return 0;
}
|
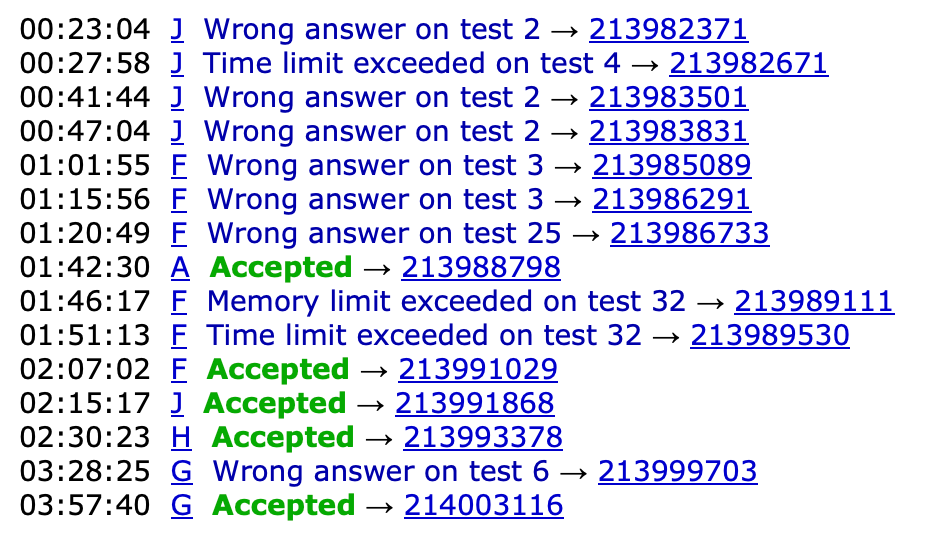
G. Gambling Guide
題意
給一張圖 $n$ 個點 $m$ 條邊
要從 $1$ 走到 $n$
每次在一個點 會均勻隨機的擲銅板選一條邊
可以選擇走 or 放棄
策略是讓擲銅板的次數越少越好
求擲銅板次數的期望值
作法
從終點開始
算每個點到終點擲銅板次數的最低期望值是多少
用 Dijkstra 的方式更新所有點
WA1: 更新期望值的時候多算還沒確定的點
submission
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
constexpr ld eps = 1e-9;
constexpr ld INF = 1e18;
bool same(ld a, ld b) {
return a-eps <= b and b <= a+eps;
}
template<typename T>
using priority_queue_greater = priority_queue<T, vector<T>, greater<T>>;
signed main() {
fast;
int n, m;
cin >> n >> m;
vector<vector<int>> G(n);
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
u--; v--;
G[u].emplace_back(v);
G[v].emplace_back(u);
}
priority_queue_greater<pair<ld,int>> pq{};
vector<ld> dist(n, INF);
vector<bool> visit(n, false);
auto push = [&](int x, ld d) {
if (d < dist[x]) {
dist[x] = d;
pq.emplace(d, x);
}
};
ld cur = 0;
auto update = [&](int x) {
int cnt = 0;
ld exp = 0;
for (auto y: G[x]) {
auto d = dist[y];
if (d <= cur + eps) {
cnt++;
exp += d;
}
}
ld d = exp / (ld)cnt + (ld)G[x].size() / (ld)cnt;
push(x, d);
};
push(n-1, 0);
while (!visit[0]) {
auto [d,x] = pq.top(); pq.pop();
if (!same(dist[x], d)) continue;
visit[x] = true;
cur = d;
for (auto y: G[x])
update(y);
}
cout << fixed << setprecision(16) << dist[0] << endl;
return 0;
}
|
H. Hidden Hierarchy
題意
給 $n$ 個檔案路徑和大小
要你輸出所有大小大於等於 $t$ 的資料夾
作法
簡單實作 (trie)
submission
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
struct Node {
int size;
map<string,Node*> child;
};
int n, mxsz;
Node* root;
void go(Node* it, string path) {
char c;
if (it->child.empty()) {
c = ' ';
} else {
auto mx = 0;
for (auto [s,nt]: it->child)
mx = max(mx, nt->size);
if (mx < mxsz)
c = '+';
else
c = '-';
}
cout << c _ path _ it->size << endl;
if (c == '-')
for (auto [s,nt]: it->child)
go(nt, path + s + '/');
}
signed main() {
fast;
root = new Node();
cin >> n;
for (int i = 0; i < n; i++) {
string path;
int size;
cin >> path >> size;
vector<string> seg;
for (int j = 1, len = 1, sz = path.size(); j+len < sz; ) {
if (path[j+len] == '/') {
seg.emplace_back(path.substr(j,len));
j = j+len+1;
len = 1;
} else {
len++;
}
}
// cerr _ path _ endl;
// for (auto s: seg) cerr _ s; cerr _ endl;
root->size += size;
auto it = root;
for (auto s: seg) {
auto nxt = it->child.find(s);
if (nxt == it->child.end())
nxt = it->child.emplace(s, new Node()).ft;
it = nxt->sd;
it->size += size;
}
}
cin >> mxsz;
go(root, "/");
return 0;
}
|
I. Intrinsic Interval (TODO)
題意
給 $1 \sim n$ 的 permutation $\pi_i$
$\pi_a^b = (\pi_a,\pi_{a+1},…,\pi_b)$
$m$ 筆詢問 $x_i, y_i$
問包含 $\pi_x^y$ 的最短 $\pi_a^b$ 滿足 $\pi_a^b$ 是連續的數字
作法 (TODO)
J. Justified Jungle
題意
給一顆 $n$ 個點的樹
問你是否有哪些 $k$ 滿足
拔掉 $k$ 條邊可以讓所有聯通塊大小一樣
$n\le 10^6$
作法
枚舉聯通塊大小 $\displaystyle\frac{n}{k+1}$
dfs 判斷子樹是否可以剛好等於 $\displaystyle\frac{n}{k+1}$
$\iff$ 判斷子樹大小為 $\displaystyle\frac{n}{k+1}$ 倍數的數量恰好 $k+1$ 個
TODO: The divisor bound
WA1: 輸出成聯通塊大小
TLE2: 可能是 $O(n \sqrt{n})$
WA34: 亂做因數分解
submission
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#define fast
#else
#define fast cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define cerr if(1);else cerr
#endif
#define _ <<' '<<
#define ALL(v) v.begin(),v.end()
#define ft first
#define sd second
using ll = long long;
using ld = long double;
using pii = pair<int,int>;
constexpr int MAXN = 1e6+5;
int sz[1000010];
vector<int> G[1000010];
int cnt[1000010];
void nene(int a, int f)
{
sz[a]=1;
for(int b:G[a])
{
if(b==f)
continue;
nene(b,a);
sz[a]+=sz[b];
}
cnt[sz[a]]++;
}
signed main() {
fast;
int n;
cin>>n;
for(int i=1;i<n;i++) {
int a,b;
cin>>a>>b;
G[a].emplace_back(b);
G[b].emplace_back(a);
}
nene(1,0);
for(int i=n-1;i>=1;i--)
{
if(n%i)
continue;
int aoi=0;
for(int j=i;j<=n;j+=i)
aoi+=cnt[j];
if(aoi==n/i)
cout<<n/i-1<<' ';
}
return 0;
}
|
K. Kitchen Knobs (TODO)
題意
給 $n$ 個圈圈
每個圈圈有 $7$ 個數字(可重複)
每次可以轉動任意數量連續的圈圈
問至少要轉幾次才可以讓所有圈圈的最大值在上面
$n\le 501$
作法 (TODO)
From presentation of solutions.
There exists a greedy $O(N)$ strategy we could follow, but it’s rather hard to find. Instead we may use a $O(N^3)$ dynamic programming to complete the assignment.
L. Lunar Landscape (TODO)
題意
給 $n$ 個正方形 or 菱形
求連集面積
$n\le 2\times 10^5$
作法 (TODO)
把正方形和菱形分開做二維前綴和
然後再枚舉 grid $2000 \times 2000 \times 4$ 判斷是否有被覆蓋